The kdtools package implements approximate nearest
neighbors. This is done in the standard way by shrinking the search
radius by a factor of \(1 / (1 +
\alpha)\). Once the greedy descent phase is completed and
candidate nearest neighbors are queued, the algorithm interrogates
adjacent half-planes while backtracking if the search key is
sufficiently close to the half-plane boundary. The factor \(\alpha\) reduces the definition of
sufficiently close. Given a sufficiently large \(\alpha\), the algorithm is entirely greedy
and ignores any points not in the nearest half-plane.
Approximate search is accomplished by setting the a
argument to a value grater than zero.
key <- runif(13)
x <- kd_sort(matrix(runif(13 * 1e5), nr = 1e5, nc = 13))
cbind(kd_nn_indices(x, key, 3, distances = TRUE),
kd_nn_indices(x, key, 3, distances = TRUE, a = 10))
#> index distance index distance
#> 1 35840 0.5607467 35908 0.6169904
#> 2 48405 0.5661820 35906 0.7226936
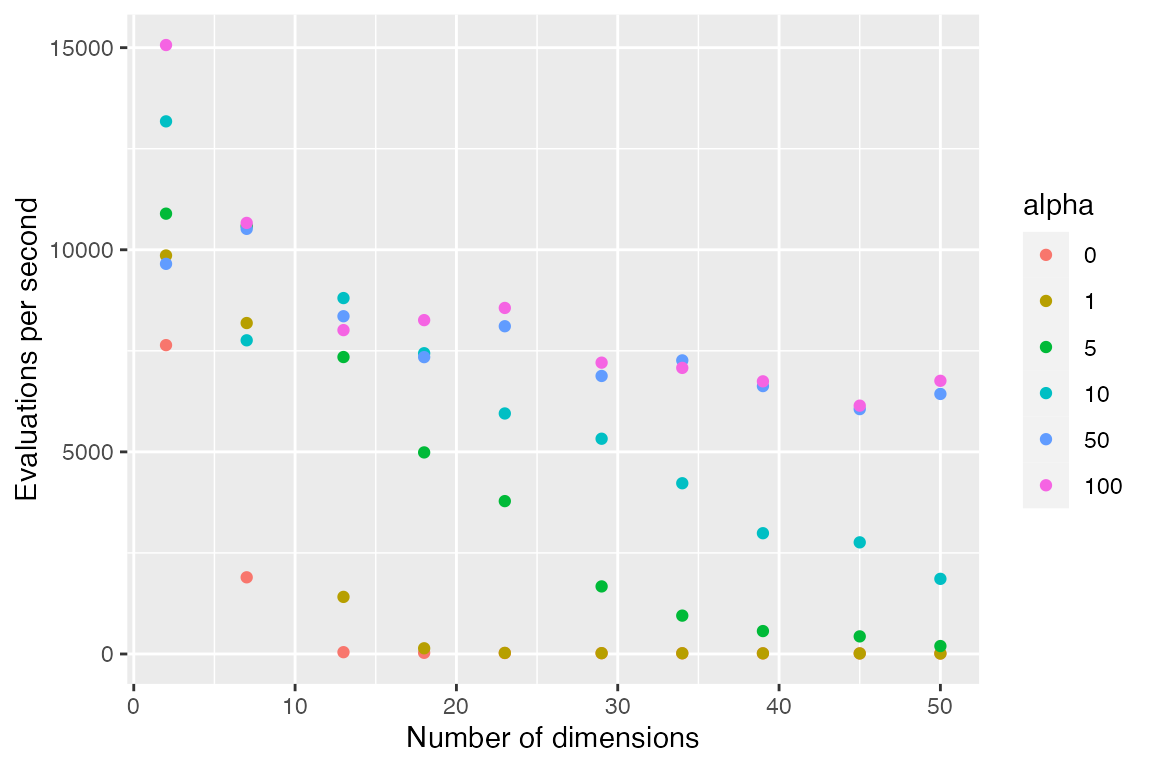
#> 3 35912 0.5796700 35915 0.7276312The results below show number of searches completed per second with different number of dimensions (length of the search key) and different values of \(\alpha\). Number of evaluations is the median of 33 trials searching among 1e+05 vectors containing uniform random deviates.
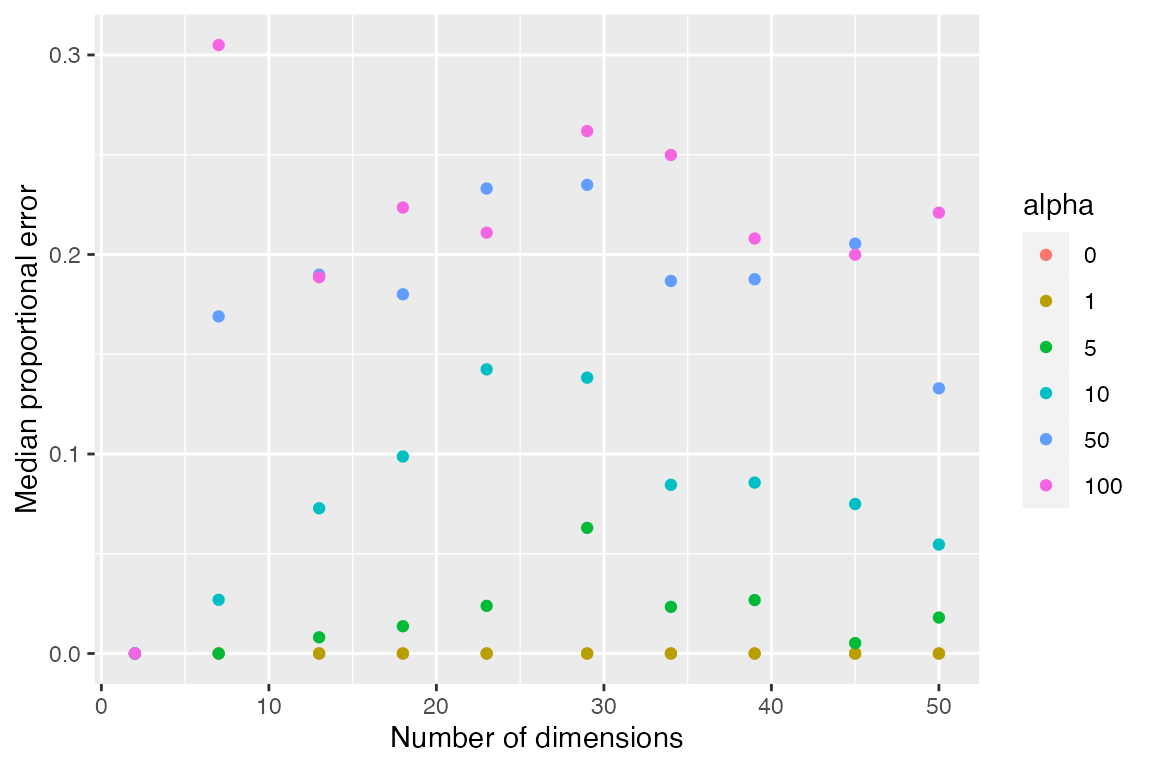
The following shows the relative error \((d_2 - d_1) / d_1\) where \(d_2\) is the approximate nearest neighbor and \(d_1\) is the exact nearest neighbor distance. Notice these results suggest that greedy search is optimal for 2-dimensions, at least for uniform random vectors. The results will depend on the details of the input data.